[单选]

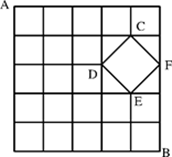
如下图所示，某城镇共有6条东西方向的街道和6条南北方向的街道，其中有一个湖，街道在此变成一个菱形的环湖大道。现要从城镇的A处送一份加急信件到B处，为节省时间，要选择最短的路线，共有（）种不同走法。

A . 35
B . 36
C . 37
D . 38

　　---------------------------------

　　参考答案：A

　　---------------------------------

　　[华图教育参考解析]：

第一步：判断题型------本题为排列组合问题

第二步：分析作答
根据三角形定理两边之和大于第三边，可以知道DE，CF小于他们所在三角形的直角边之和，因此路过DE或CF时路线最短。
分情况讨论
当从A经过DE到B时，A到D最短需要走5步，选出两个南北方向的路段共有种，
E到B最短需要3步，从选除两个东西方向的路段共有种，则共有10×3=30种。
当从A经过CF到B时，A到C最短需要走5步，选出1个南北方向的路段共有种，
F到B最短需要3步，且只有一种情况最短，则共有5种。因此共有5+30=35种走法。

故本题选A。
【2010-上海-089】